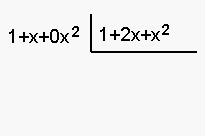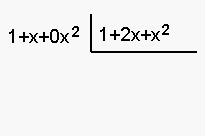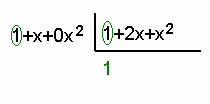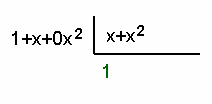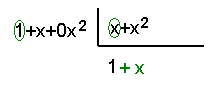Algoritmo para la
División de Polinomios en Matlab
hay un método para dividir
polinomios llamado "División Larga" en el cual se basan ciertas
igualdades con series de sumas infinitas de series de potencias.
Por ejemplo esta serie:
1/(1 - x) = 1 + x + x2 + x3
+ ...
Para hacer esta división
los polinomios se deben ordenar de menor a mayor grado, en el caso de una
división simple como (x2+2x+1)/(x+1) se coloca de esta forma:
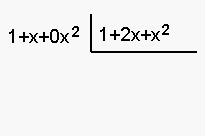
Sí, el numerador y el
denominador se colocan al revés de cómo normalmente se colocan al hacer la
división. Bueno así nos enseñó el profe de PDS y así está basado el
algoritmo...
Para el primer término (en
este caso el de menor grado) del cociente se divide el término de menor grado
del numerador entre el término de menor grado del denominador:
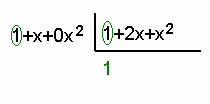
Luego se multiplica el
denominador por eeste primer término del cociente y se resta al numerador:
(1+2x+x2)-(1+x)=x+x2
por lo que la nueva
división será entre:
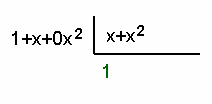
Y se vuelve a dividir el
término de menor grado del nuevo numerador entre el término de menor grado del
denominador:
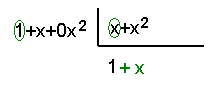
Luego se multiplica el
denominador por el término del cociente recién calculado (en verde) y se resta
al numerador:
(x+x2)-(x+x2)=0
Esto se repite hasta que ya
no queda numerador. El coeficiente se obtiene término a término y en este
punto ya lo tenemos.
En el caso de 1/(1-x) se
generará una suma polinómica infinita pues siempre habrá numerador con el
qué dividir.
He aquí el algoritmo ya
comentado:
%Algoritmo para realizar la "División Larga"
%programado por Yelinna Pulliti Carrasco
%https://toyscaos.tripod.com/eam.html
ex = input('ingresar el mayor grado de los polinomios: ');
% si se tiene por ejemplo (0.5-3x^2)/(2 + x + x^3) se debera ingresar 3
Hd = zeros(1,30); %contendra los coeficientes del denominador
Hn = zeros(1,30); %contendra los coeficientes del numerados
Hc= zeros(1,30); %contendra los coeficientes del cociente
% la longitud de estos vectores puede hacerse mas o menos larga a
% conveniencia, he puesto arbitrariamente 30 pero puede ser cualquier
% numero, esto es porque hay divisiones polinomicas que generan sumas
% infinitas.
Hn(1)= input('ingrese el termino independiente del numerador: '); % para el ejemplo anterior seria 0.5
while Hn(1) ==0 %si este termino es cero, el polinomio no es irreductible
Hn(1)= input('dato no valido, debe ser diferente de 0. Ingrese otro valor: ') ;
end;
for k = 2:ex+1
Hn(k) = input(strcat('ingrese el ', int2str(k-1), '° coeficiente del numerador: '));
end; % en el caso del numerador los numeros a ingresar son: 0.5 , 0 y -3
disp('2do polinomio: ');
Hd(1)= input('ingrese el termino independiente del denominador: '); % para el ejemplo seria 2
while Hd(1) ==0
Hd(1)= input('dato no valido, debe ser diferente de 0. Ingrese otro valor: ') ;
end;
for k = 2:ex+1
Hd(k) = input(strcat('ingrese el ', int2str(k-1), '° coeficiente del denominador: '));
end; % en el caso del denominador los numeros a ingresar son: 1 , 0 y 1
% este algoritmo se deduce del metodo para dividir polinomios que genera
% sumas infinitas si el resultado no es exacto, por ello nunca se generara
% un residuo. Este tipo de division es muy util en el caso que se tengan
% que generar series de potencias y se conoce como "División larga"
% Recomiendo probarlo con 1/(1-x) y haciendo que la longitud de los
% vectores Hn, Hc y Hd sea mucho mayor.
Hc(1) = Hn(1)/Hd(1);
for i=2:length(Hn)
Hn(i-1)=0; kk= 2;
for j=i:length(Hn)
Hn(j) = Hn(j)-Hc(i-1)*Hd(kk);
kk= kk+1;
end;
Hc(i) = Hn(i)/Hd(1);
end;
disp('Los sumandos del cociente son: ');
for i = 1:length(Hc)
if Hc(i)==0
continue;
else
disp(strcat(int2str(Hc(i)), 'x^', int2str(i-1) ));
end;
end; |
La condición es que el denominador y
tenga un término independiente, es preferible que numerador y denominador sean
irreductibles.